ヒストリカルボラティリティをエクセルで算出するには、STDEV関数の使い方と年率換算のための√250が重要です。
実際にエクセルを用いて算出してみましょう。
【目次】
1.ヒストリカルボラティリティ(HV)とは
2.エクセルに書き込む関数
3.インプライドボラティリティとの関連性
4.まとめ
1.ヒストリカルボラティリティ(HV)とは
ヒストリカルボラティリティとは、過去の原資産価格の変動割合を年率で表した数値となります。
一般的にヒストリカルボラティリティの調査期日に指定が無い場合は20日平均HVである場合が最も多く、20日平均HVとは、過去20日の値動きのばらつきを年率にしたもの、となります。
2.エクセルに書き込む関数
エクセルに入れる式
=STDEV{LN(今日の終値/昨日の終値),LN(昨日の終値/2日前の終値),LN(2日前の終値/3日前の終値),LN(3日前の終値/4日前の終値),LN(○日前の終値/○+1日前の終値),・・・,LN(20日前の終値/21日前の終値)}×√250
です。では数式の解説をします。
標準偏差
標準偏差=STDEV(LN(今日の終値/昨日の終値),LN(昨日の終値/一昨日の終値)・・・・LN(20日前の終値/21日前の終値))
と計算することで、標準偏差が求まります。
STDEV関数の中身
エクセルでは標準偏差を求めるSTDEVという関数を使い、過去の値動きの標準偏差(シグマ)を求めます。
なお、ボラティリティを求めるときは、【昨日からの変動率】を拾う必要があるので、【今日の終値÷昨日の終値】を入力します。
さらに日経平均の変動は【連続複利で表わされる】と定義しています。
連続複利とは、複利回数が無限大で連続的に元本に繰入れられると仮定した場合の収益率のこと
この連続複利の計算にはエクセルのLNという関数を使います。LNというのは自然対数を求める式です。
STDEVの記載事例
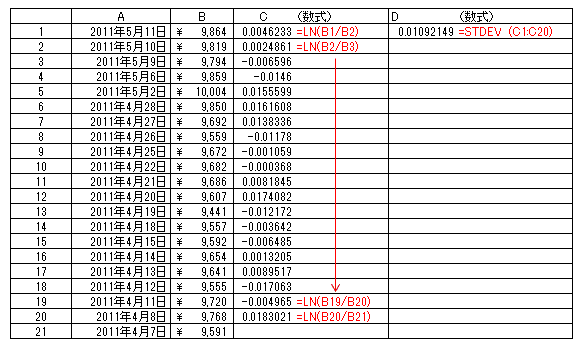
具体的にエクセルのセルで表すと下図のようになります。
エクセルは式を手入力で打ち込むより、一定の規則で入力すると非常に手間が省けます。C列の数式も一番上を作ったらセルの右下をつまんでドラッグすると自動的に関数が入ります。
年率換算
STDEVで算出された標準偏差は、1日当たりのHVを表しています。
ヒストリカルボラティリティは年率なので、年単位に換算するため、営業日である250日に平方根を付けます。
平方根にする理由は、分散を表すσ^2が時間と比例するからです。
3.インプライドボラティリティとの関連性
さて、このようにエクセルでヒストリカルボラティリティを算出すると、この数値は過去の価格のみを参照しているということです。
一方でオプション投資にはインプライドボラティリティがあります。
このインプライドボラティリティは、将来の価格の予想を暗示していると言われて、オプション投資ではヒストリカルボラティリティよりも重要視されます。
インプライドボラティリティの構成要素
そのインプライドボラティリティは下記の構成要素で決まります。
- 原資産価格
- オプション価格
- 権利行使価格
- 残存日数
- 金利
以上のように、インプライドボラティリティについては過去の価格は一切関係が無く、最も重要なのは現在のプレミアム、つまりオプション価格となります。
オプション価格から逆算したボラティリティがインプライドボラティリティであり、この数値を参照しながらオプション価格が割高なのか割安なのかを判断することが出来ます。
ヒストリカルボラティリティから将来を予測出来ない
このインプライドボラティリティですが、ヒストリカルボラティリティから予測することはできません。
未来を予想するのに過去の数値を見ても将来は予測できないのです。
しかしながら、過去のこれまでの値動きを把握するためにヒストリカルボラティリティは有効かもしれません。
実際のところインプライドボラティリティとヒストリカルボラティリティは似たような変動を示す場合もあります。ですがあくまで過去の値動きの変動を示しているにすぎないので、バックミラーを見ながら前方の道路を予測している運転手のようなものになります。
ハイウェイのような一直線の道を進むのにはバックミラーでも運転は可能かも知れませんが、曲がり角があったとしてもバックミラーを見ているだけでは事故を回避するのは不可能です。
将来を予測し、将来の変動を利益の原資とすべくトレードするのであれば、過去を見るのではなく現在、未来を予測した値を採用したいと思いますよね。
4.まとめ
エクセルを利用するとヒストリカルボラティリティは非常に簡単に算出できることがわかります。
しかしながら、ヒストリカルボラティリティはバックミラーを見るがごとく過去の数値の参照に過ぎません。
これから将来の変動を利益に変えると考えた場合にはインプライドボラティリティの特性も理解してトレードに生かした方が有益だと考えられます。
オプション取引に興味が湧きましたら、ぜひメルマガ登録をしてくださいね。